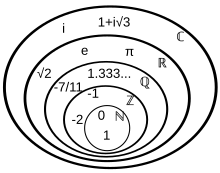
Number
mathematical object used to count, label, and measure
A number is a mathematical object used to count, measure, and label.
Addition
edit1.
2.
3.
Subtraction
edit1.
2.
3.
Quotes
edit- Ten is the nature of number. All Greeks and all barbarians alike count up to ten, and having reached ten revert again to the unity. And again, Pythagoras maintains, the power of the number 10 lies in the number 4, the tetrad. This is the reason: if one starts at the unit (1) and adds the successive number up to 4, one will make up the number 10 (1+2+3+4 = 10). And if one exceeds the tetrad, one will exceed 10 too.... So that the number by the unit resides in the number 10, but potentially in the number 4. And so the Pythagoreans used to invoke the Tetrad as their most binding oath: "By him that gave to our generation the Tetractys, which contains the fount and root of eternal nature..."
- Aëtius of Antioch Aëtius (c. 350) [I. 3.8]
- Pythagoras... assumed as first principles the numbers and symmetries existing among them, which he calls harmonies, and the elements compounded of both, that are called geometrical. ...he says that the nature of Number is the Decad.
- Aëtius of Antioch Aëtius (c. 350) [I. 3.8] as quoted by Keith Critchlow in the Forward to The Theology of Arithmetic by Iamblichus (1988) Tr. Robin Waterfield, p. 9.
- If the early Greeks were cognizant of Babylonian algebra, they made no attempt to develop or even to use it, and thereby they stand convicted of the supreme stupidity in the history of mathematics. ...The ancient Babylonians had a rare capacity for numerical calculation; the majority of Greeks were either mystical or obtuse in their first approach to number. What the Greeks lacked in number, the Babylonians lacked in logic and geometry, and where the Babylonians fell short, the Greeks excelled. Only in the modern mind of the seventeenth and succeeding centuries were number and form first clearly perceived as different aspects of one mathematics.
- Eric Temple Bell, The Development of Mathematics (1940)
- With the intrusion of irrational numbers to disrupt the integral harmonies of the Pythagorean cosmos, a controversy that has raged off and on for well over two thousand years began: is the mathematical infinite a safe concept in mathematical reasoning, safe in the sense that contradictions will not result from the use of this infinite, subject to certain prescribed conditions?
- Eric Temple Bell, The Development of Mathematics (1940)
- [T]he invention of writing... occurred somewhere around 3000 B.C. This is attributed to the Sumerians... Sarton mentions that about one hundred clay tablets are known... that refer to Sumerian mathematics and table of numbers. These include tables of squares and cubes, square roots and cube roots, reciprocals and multiplication tables. The Sumerians had originated a decimal system. They seem to have had a natural genius for algebra and were certainly able to solve linear, quadratic and cubic equations. Their most surprising achievement was their handling and understanding of negative numbers, a concept that did not penetrate Western minds until centuries later.
- Aubrey F. Burstall, A History of Mechanical Engineering (1965)
- By the ancients [Greeks], arithmetic was studied through geometry. If a number was regarded as simple, it was a line. If as composite, it was a rectangular figure. To multiply was to construct a rectangle, to divide was to find one of its sides. Traces of this still remain in such terms as square, cube, common measure, but the method itself is obsolete. Hence, it requires an effort to conceive of the square root, not as that which multiplied into itself produces a given number, but as the side of a square, which [square area] either is the number, or is equal to the rectangle which is the number.
- Lewis Campbell, The Theaetetus of Plato (1861) p. 19.
- For measurements of time he collected and weighed water flowing from a container at a constant rate of about three fluid ounces per second, He recorded weights of water in grains and, and defined his time unit, called a tempo, to be the time for 16 grains of water to flow, which was equivalent to 1/92 second. These units were small enough so Galileo's measurements of distance and time always resulted in large numbers. That was a necessity because decimal numbers were not part of his mathematical equipment; the only way he could add significant digits in his calculations was to make the numbers larger.
- William H. Cropper, Great Physicists (2004)
- The arithmetization of mathematics... which began with Weierstrass... had for its object the separation of purely mathematical concepts, such as number and correspondence and aggregate, from intuitional ideas, which mathematics had acquired from long association with geometry and mechanics.
These latter, in the opinion of the formalists, are so firmly entrenched in mathematical thought that in spite of the most careful circumspection in the choice of words, the meaning concealed behind these words, may influence our reasoning. For the trouble with human words is that they possess content, whereas the purpose of mathematics is to construct pure thought.- Tobias Dantzig, Number: The Language of Science (1930)
- In speaking of arithmetic (algebra, analysis) as a part of logic I mean to imply that I consider the number concept entirely independent of the notions or intuitions of space and time, that I consider it an immediate result from the laws of thought. My answer to the problems propounded in... this paper is... briefly this: numbers are free creations of the human mind; they serve as a means of apprehending more easily and more sharply the difference of things. It is only through the purely logical process of building up the science of numbers and by thus acquiring the continuous number-domain that we are prepared accurately to investigate our notions of space and time by bringing them into relation with this number domain created in our mind.
- Richard Dedekind, Essays on the Theory of Numbers (1901) Tr. Wooster Woodruff Beman, Preface to the First Edition.
- In Greek theoretical mathematics (as distinguished from practical or commercial arithmetic) a fraction that we would write as a/b was not regarded as a number, as a single entity, but as a relationship or ratio a : b between the whole numbers a and b. Thus the ratio a : b was, in modern terms, simply an ordered pair, rather than a rational number.
- C. H. Edwards, Jr., The Historical Development of the Calculus (1979)
- In past centuries it was widely accepted that an understanding of, as well as a facility with numbers, is an essential part of an education. ...This book has been written with an intention of showing that numbers have been the centre of man's awareness of his surroundings since well before any times of which we have surviving records. It will show that numbers have provided an answer to man's cultural needs at least since any form of organized human society came into being.
- Graham Flegg, Numbers: Their History and Meaning (1983).
- It is fair to claim that it is a student's understanding of mathematics, above all other subjects, which suffers most from unenlightened teaching methods. ...the troubles may well stem mainly from the first year or two of the child's encounter with numbers... if children come to fear them or to be bored with them, they will eventually join the ranks of the present majority for whom the word 'mathematics' is guaranteed to bring social conversation to an immediate halt. If, on the other hand, numbers are made a genuine source of adventure and exploration from the beginning, there is a good chance that the level of numeracy in society can be raised significantly. There is a real role here for the history of mathematics—and the history of number in particular—for history emphasizes the diversity of approaches and methods which are possible and frees us from the straightjacket of contemporary fashions in mathematics education. It is, at the same time, both interesting and stimulating in its own right.
- Graham Flegg, Numbers: Their History and Meaning (1983).
- I esteem myself happy to have as great an ally as you in my search for truth. I will read your work … all the more willingly because I have for many years been a partisan of the Copernican view because it reveals to me the causes of many natural phenomena that are entirely incomprehensible in the light of the generally accepted hypothesis. To refute the latter I have collected many proofs, but I do not publish them, because I am deterred by the fate of our teacher Copernicus who, although he had won immortal fame with a few, was ridiculed and condemned by countless people (for very great is the number of the stupid).
- Galileo Galilei, letter to Johannes Kepler (1596), as quoted in The Story of Civilization : The Age of Reason Begins, 1558-1648 (1935) by Will Durant, p. 603.
- My purpose is to set forth a very new science dealing with a very ancient subject. There is, in nature, perhaps nothing older than motion, concerning which the books written by philosophers are neither few nor small; nevertheless I have discovered by experiment some properties of it which are worth knowing and which have not hitherto been either observed or demonstrated. Some superficial observations have been made, as, for instance, that the free motion [naturalem motum] of a heavy falling body is continuously accelerated; but to just what extent this acceleration occurs has not yet been announced; for so far as I know, no one has yet pointed out that the distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity.
- Galileo Galilei, Dialogues and Mathematical Demonstrations Concerning Two New Sciences (1638) Third Day. Change of Position (De Motu Locali), Tr. Henry Crew & Alfonso de Salvio (1914) p.153.
- It was Pythagoras who discovered that the 5th and the octave of a note could be produced on the same string by stopping at 2⁄3 and ½ of its length respectively. Harmony therefore depends on a numerical proportion. It was this discovery, according to Hankel, which led Pythagoras to his philosophy of number. It is probable at least that the name harmonical proportion was due to it, since
1:½ :: (1-½):(2⁄3-½). - James Gow, A Short History of Greek Mathematics (1884) p. 68, Footnote, citing Vide Cantor, Vorles [Vorlesüngen über Geschichte der Mathematik ?] p 152. Nesselmann p. 214 n. Hankel. p. 105 sqq.
- Some fundamental unity was surely to be discerned either in the matter or the structure of things. The Ionic philosophers chose the former field: Pythagoras took the latter. ...The geometry which he had learnt in Egypt was merely practical. ...It was natural to nascent philosophy to draw, by false analogies, and the use of a brief and deceptive vocabulary, enormous conclusions from a very few observed facts: and it is not surprising if Pythagoras, having learnt in Egypt that number was essential to the exact description of forms and of the relations of forms, concluded that number was the cause of form and so of every other quality. Number, he inferred, is quantity and quantity is form and form is quality.
- James Gow, A Short History of Greek Mathematics (1884) pp. 67-68.
- Now any one who was in the habit of intently studying the heavens would naturally observe that each constellation has two characteristics, the number of the stars which compose it and the geometrical figure which they form. Here, as a recent writer [Léon Brunschvicg, Lea étapes de la philosophic mathématique] has remarked, we find, if not the origin, a striking illustration of the Pythagorean doctrine. And, just as the constellations have a number characteristic of them respectively, so all known objects have a number; as the formula of Philolaus states, 'all things which can be known have number; for it is not possible that without number anything can either be conceived or known.'
- Thomas Little Heath, A History of Greek Mathematics (1921) Vol. 1, p. 67.
- In communicating information about different sorts of things in the world, primitive man first learned to substitute crude pictures for speech to record seasonal occurrences for future use. ...As time went on the pictorial character of writing became less recognizable. ...The broad division between two kinds of writing... has its parallel in mathematics. The literature of mathematics begins with the pictorial or hieroglyphic language which we call geometry. ...At a much later date people stopped using nothing but pictures to record how numbers behave. They began to use letters, and compiled dictionaries in which you can find the meaning of the words used. Such dictionaries are called tables. ...Dictionary language, or, as mathematicians call it, "analysis," came later than hieroglyphic language, and grew out of it; but it has never supplanted the need for it completely.
- Lancelot Hogben, Mathematics for the Million (1936).
- Bourgeois society is ruled by equivalence. It makes dissimilar things comparable by reducing them to abstract quantities. For the Enlightenment, anything which cannot be resolved into numbers, and ultimately into one, is illusion; modern positivism consigns it to poetry.
- Max Horkheimer and Theodor W. Adorno, Dialectic of Enlightenment E. Jephcott, trans., p. 4
- C'est de l'Inde que nous vient l'ingénieuse méthode d'exprimer tous les nombres avec dix caractères, en leur donnant à la fois, une valeur absolue et une valeur de position; idée fine et importante, qui nous paraît maîntenant si simple, que nous en sentons à peine, le mérite. Mais cette simplicité même, et l'extrême facilité qui en résulte pour tous les calculs, placent notre système d'arithmétique au premier rang des inventions utiles; et l'on appréciera la difficulté d'y parvenir, si l'on considère qu'il a échappé au génie d'Archimède et d'Apollonius, deux des plus grands hommes dont l'antiquité s'honore.
- It is India that gave us the ingenious method of expressing all numbers using ten characters, giving these numbers simultaneously a value absolute and a value of position; a fine and important idea, which seems so simple now, that we hardly appreciate its merit. But this very simplicity, the extreme ease resulting in all calculations, place our system of arithmetic in the first rank of useful inventions; and we appreciate the difficulty of achieving this, considering that it escaped the genius of Archimedes and Apollonius, two of the greatest and most honored men of antiquity.
- Pierre-Simon Laplace, Exposition du Système du Monde, Vol. 2 (1798) also quoted in Tobias Dantzig, Number: The Language of Science (1930).
- If the Greeks had had a mind to reduce mathematics to one field... their only choice would have been to reduce arithmetic to geometry... it is hardly surprising that for nearly two millennia geometry took pride of place in mathematics. And it would have been obvious to any mathematician that a geometrical problem could not be stated or solved in the language of numbers, since the geometrical universe had more structure than the numerical universe.
If one desired to translate geometrical problems into the language of numbers, one would have to invent (or discover) more numbers.- Tim Maudlin, New Foundations for Physical Geometry: The Theory of Linear Structures (2014) p. 12.
- Plato denied explicitly the existence of fractional numbers: the numerical unit had no parts and could not be divided. Of course, for practical purposes fractions were commonly required. The use of what we call rational numbers therefore infiltrated almost imperceptibly into theoretical mathematics. It would be hard to say exactly when rational numbers were recognized as numbers, since this requires making a careful distinction between the ratio 1:2 (which had a perfectly good pedigree in Eudoxus' theory of proportion) and the number ½. ...It would be quite a long time after this period before irrational numbers were tolerated, and until this step was taken there was no prospect for describing geometrical problems in arithmetical terms.
- Tim Maudlin, New Foundations for Physical Geometry: The Theory of Linear Structures (2014) p. 13.
- Every measurable thing except numbers is imagined in the manner of a continuous quantity. Therefore, for the mensuration of such a thing, it is necessary that points, lines, and surfaces, or their properties, be imagined. For in them... measure or ratio is initially found... Therefore, every intensity which can be acquired successively ought to be imagined by a straight line perpendicularly erected on some point of the space or subject of the intensible thing, e.g., a quality... And since the quantity or ratio of lines is better known and is more readily conceived by us—nay the line is in the first species continua, therefore such intensity ought to be imagined by lines... Therefore, equal intensities are designated by equal lines, a double intensity by a double line, and always in the same way if one proceeds proportionally.
- Nicole Oresme, Treatise on the Configuration of Qualities and Motions (c. 1350) Tr. Marshall Clagett in Nicole Oresme and the Medieval Geometry of Qualities and Motions: A Treatise on the Uniformity and Difformity of Intensities Known as "Tractatus de configurationibus et qualitatibus et motuum" (1968) Ch. 1-2.
- [Number is] the commanding and self-begotten container of the eternal duration of mundane concerns.
- Philolaus (c. 420 BCE) as quoted by Aristotle, Metaphysics (ca. 350 BC) Tr. Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid's Elements (1792) Vol. 1, p. xix.
- [A]ll things which can be known have number; for it is not possible that without number anything can either be conceived or known.
- Philolaus (c. 420 BCE) as quoted by Thomas Little Heath, A History of Greek Mathematics (1921) Vol. 1, p. 67, citing (Stob Ecl. i. 21, 7b (Vors. i3, p. 310. 8-10)
- All things, at least those we know, contain number; for it is evident that nothing whatever can either be thought or known, without number. Number has two distinct kinds: the odd, and the even, and a third, derived from a mingling of the other two kinds, the even-odd. Each of its subspecies is susceptible of many very numerous varieties; which each manifests individually.
- Philolaus, as quoted by Iamblichus, Fragments of Philolaus, Fragment 2, The Life of Pythagoras (1919) Tr. Kenneth Sylvan Guthrie from August Boeckh, Philolaos des Pythagoreers Lehren nebst den Bruchstücken seines Werkes (1819).
- Number is the ruler of forms and ideas, and the cause of gods and daemons.
- Pythagoras, as quoted in Life of Pythagoras (c. 300) by Iamblichus of Chalcis, Tr. Thomas Taylor (1818)
- Number rules the universe.
- Pythagoras, as quoted in The Story of a Number (1905) by E. Maor; also quoted by Desmond MacHale, Comic Sections (1993)
- In a rough way we may summarize the conclusions of the writers to whom reference has chiefly been made, as follows:
1. Let the child learn to count things, thus getting the notion of number. These things are, for the purpose of counting, considered alike, and they may be single objects or groups.
2. Let him acquire the number series, exercising with it beyond the circle of actually counted things.
3. In the learning of symbols it does not seem to be a matter of moment as to whether these are given with the first presentation of number or not. They must, however, be acquired soon.
4. Unconsciously and gradually the child will acquire the idea (never expressed to him in words) of the one-to-one correspondence of number, name, symbol, and thereafter the pure concept of number will play a small part in his arithmetical calculations.
5. The ratio idea of number should be introduced early, and applied in the work with fractions.- David Eugene Smith, The Teaching of Elementary Mathematics (1904) pp. 108-109.
- Number, its kinds; the first kind, intellectual in the divine mind.
Number is of two kinds, the Intellectual (or immateriall) and the Scientiall. The intellectuall is that eternal substance of number, which Pythagoras in his discourse concerning the Gods asserted to be the principle most providentiall of all Heaven and Earth, and the nature that is betwixt them. Moreover, it is the root of divine Beings, and of gods, & of Dæmons. This is that which he termed the principle, fountain,and root of all things, and defined it to be that which before all things exists in the divine mind; from which and out of which all things are digested into order, and remain numbred by an indissolube series.
For all things which are ordered in the world by nature according to an artificiall course in part and in whole appear to be distinguished and adorn'd by Providence and the All-creating Mind, according to Number; the exemplar being established by applying (as the reason of the principle before the impression of things) the number præxistent in the Intellect of God, maker of the world. This only in intellectual, & wholly immaterial, really a substance according to which as being the most exact artificiall reason, all things are perfected, Time, Heaven, Motion, the Stars and their various revolutions.
...The other kind of number, Scientiall; its principles.
Scientiall Number is that which Pythagoras defines the extension and production into act of the seminall reasons which are in the Monad, or a heap of Monads, or a progressian of multitude beginning from Monad, and a regression ending in Monad.- Thomas Stanley, The History of Philosophy, the Third and Last Volume, in Five Parts. (1660) The First Part, Containing the Italick Sect. pp.54-55
- It is properly debated whether irrational numbers are true numbers or fictions. For if we lack rational numbers in geometrical figures, their place is taken by irrationals, which prove precisely those things that rational numbers could not; certainly from the demonstrations they show us we are moved and compelled to admit that they really exist from their effects, which we perceive to be real, sure, and constant.
On the other hand, other things move us to a different assertion, namely that we are forced to deny that irrational numbers are numbers. Namely, where we might try to subject them to numeration [decimal representation] and to make them proportional to rational numbers, we find that they flee perpetually, so that none of them in itself can be freely grasped: a fact that we perceive in the resolving of them... Moreover, it is not possible to call that a true number which is such as to lack precision and which has no known proportion to true numbers. Just as an infinite number is not a number, so an irrational number is not a true number and is hidden under a sort of cloud of infinity. And thus the ratio of an irrational number to a rational number is no less uncertain than that of an infinite to a finite.- Michael Stifel, Arithmetica Integra (1544) as quoted by Peter Pesic, Music and the Making of Modern Science (2014)
- [Gottlob Frege] had set himself the task of defining the fundamental concept of arithmetic—i.e. number—in terms that succeeded in 'stripping off' all the 'irrelevant accretions that veil it from the eye of the mind', and so displaying it 'in its pure form'. For his purposes, it was beside the point to ask how men's actual use of number-conceptions had developed historically, or what differences anthropologists had found between the methods of counting and figuring used in different cultures; such factual studies merely chronicled the changing meanings of number-words in our historical gropings towards fully adequate or 'pure' number-conceptions. A rationally based arithmetic, by contrast, must concern itself with the ideal and final system of number-concepts, and this will provide a unique intellectual standard, or template, for judging all men's earlier and cruder proto-arithmetical creations. The analysis of number concepts must therefore be undertaken using the instruments of logic alone. It calls for the construction and interpretation of a rigorous axiomatic system already being worked out for arithmetic by... Peano.
Frege's Foundations of Arithmetic served as a philosophical example which was soon followed by others. The program... became a model for Bertrand Russell's work on philosophical logic, and for half a century's research on philosophy of science...- Stephen Toulmin, Human Understanding, Vol. 1 The Collective Use and Evolution of Concepts (1972) pp. 56-57.
- The "computable" numbers may be described briefly as the real numbers whose expressions as a decimal are calculable by finite means. ...According to my definition, a number is computable if its decimal can be written down by a machine. ...I show that certain large classes of numbers are computable. They include, for instance, the real parts of all algebraic numbers, the real parts of the zeros of the Bessel functions, the numbers π, e, etc. The computable numbers do not, however, include all definable numbers. ...[C]onclusions are reached which are superficially similar to those of Gödel. ...[I]t is shown ...that the Hilbertian Entscheidungsproblem can have no solution. In a recent paper Alonzo Church... reaches similar conclusions...
- Alan Turing, "On Computable Numbers, with an Application to the Entscheidungsproblem" (1936) Proceedings of the London Mathematical Society, Vol. 2-42, Issue 1, pp. 230-265. Note: the Gödel reference is to "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I" (1931).
- The evolution of number into the 'transfinite' was included only to emphasize the power of the forces acting within mathematics to compel this development—even against the philosophy of its most prominent creator, George Cantor (...numbers were extended, along with their arithmetic, to the non-finite, not as a mathematical whim, but for reasons of strong internal stresses.)
- Raymond Louis Wilder, Evolution of Mathematical Concepts: An Elementary Study (1975)
- In regard to Philolaus, we are told... that he derived geometrical determinations (the point, the line, the surface, the solid) from the first four numbers, so he derived physical qualities from five, the soul from six; reason, health, and light, from seven; love, friendship, prudence, and inventive faculty from eight. Herein (apart from the number schematism) is contained the thought that things represent a graduated scale of increasing perfection; but we hear nothing of any attempt to prove this in detail, or to seek out the characteristics proper to each particular region.
- Eduard Zeller, A History of Greek Philosophy from the Earliest Period to the Timee of Socrates (1881) Tr. Sarah Frances Alleyne Vol. 1, p. 475.
- Philosopher of science Keith Devlin is wrong to aver that numbers "arise from the recognition of patterns in the world around us." They arise because they are necessary for running a certain kind of society; number has only an imposed relationship to what is found in the world. Math historian Graham Flegg makes a similar error when he asserts, "Numbers reveal the unity which underlies all of life as we experience it." The "unity" in question did not exist before it was produced, with the invaluable assistance of number.
- John Zerzan, Why Hope?: The Stand Against Civilization (2015), p. 14
- For Plato, the first upward steps out of the cave toward wisdom begin with mastery of the arts of number. This put thought on the path of representation and mathematical objectification. Mathematics' more concrete, everyday rule—to serve the needs of power—makes this path the history of oppression.
- John Zerzan, Why Hope?: The Stand Against Civilization (2015), p. 15
See also
editExternal links
edit- Number @Encyclopedia of Mathematics